

- SOLUTION VECTORS FOR SPARSE LINEAR EQUATION SYSTEMS FULL
- SOLUTION VECTORS FOR SPARSE LINEAR EQUATION SYSTEMS SOFTWARE

Please note that I had already copied (A,x,b) to GPU via CuArray constructs and fed these to CUSOLVER.csrlsvqr!, so the HtoD memcpy is confusing to me. The only thing I found was CUSOLVER.csrlsvqr! which takes a staggering 4seconds, which I profiled and noticed that 49% of time is spent on “void csqr_leftLooking” and 47% on “CUDA memcpy HtoD”.
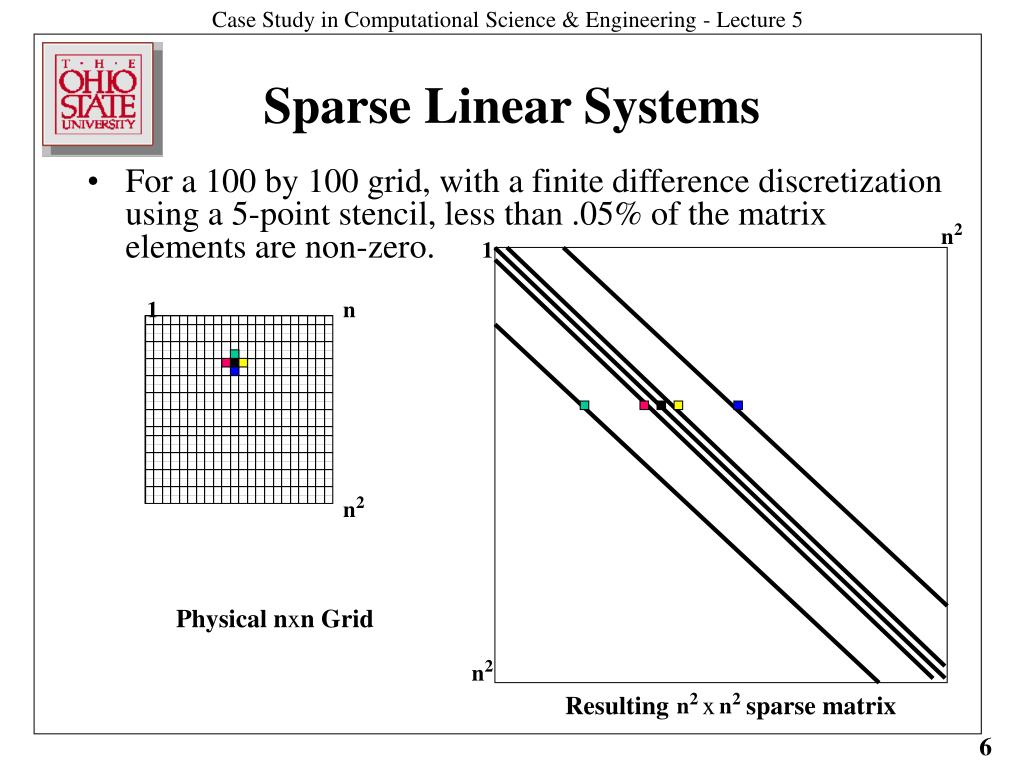
Using CUDA.jl I am unable to use the backslash operator as it does not work for SparseMatrixCSR. I want to parallelize this in hopes of getting a faster solve time. Strangely (or maybe I am missing something) when I change the values in t_num_threads I see no difference in the timings reported by macro. Numerous scientific, engineering, and smart city applications require the solution of sparse linear systems 1,2,3,4,5. It takes around 0.05 seconds for the ldiv! step. Parallel sparse matrixalgorithms are excluded, yet they too rely on the theory discussed here. Finding a solution to sparse linear equation systems is at the core of scientific computing. I use LU decomposition for A and pass this to ldiv!. Form the augmented matrix for the matrix equation ATAx ATb, and row reduce. Here is a method for computing a least-squares solution of Ax b: Compute the matrix ATA and the vector ATb. Let A be an m × n matrix and let b be a vector in Rn. A is constant throughout my simulation, while b changes at every step in my loop, and I have recalculate x once b changes. Recipe 1: Compute a Least-Squares Solution. Suppose there is an equation in system involving only one unknown solution component (i.e., only one entry in that row of matrix is nonzero). But this is inefficient and it is useful to preallocate the storage size.I want to solve Ax = b where A is a sparse matrix of size 10^5 x 10^5 (around 18 non-zero entries per row), x and b are vectors. 22.3 Iterative Techniques Applied to Sparse Matrices A is the matrix of the linear system and it must be square. The solutions to the system T(x) b are given by xp + ker(T) where xp is a particular solution to T(x) b. PETSc can dynamically grow sizes needed to store matrix entries. We want to have a tridiagonal matrix, so will have two entries in the first and last row, and three entries in each other row. Let’s get started and specify a matrix of dimension 1000 x 1000. In this example we do not use the parallel features of PETSc and refer to the documentation for details. PETSc by default uses the CSR matrix format and distributes rows across different compute nodes. This paper presents an algorithm that solves linear systems in sparse matrices asymptotically faster than matrix multiplication for any omega > 2 and. Typically, we create a sparse matrix in three steps. The main object in PETSc for creating sparse matrices is the MAT object.
SOLUTION VECTORS FOR SPARSE LINEAR EQUATION SYSTEMS SOFTWARE
While Scipy is well suited for smaller and medium sized problems, PETSc is ideal if software is meant to eventually scale across clusters of computers. In this notebook we want to demonstrate some of the features of PETsc for the solution of sparse linear systems of equations. It has powerful data structures to scale computations from simple workstations to petascale clusters. PETSc is a widely used software for the solution of linear and nonlinear systems of equations arising from PDE discretisations. Using petsc4py for sparse linear systems # Cholesky factor sparsity pattern can be derived from matrix sparsity pattern. Iterative Solvers 3 - The Conjugate Gradient MethodĪssignment 1 - Matrix-matrix multiplicationĪssignment 4 - Solving a finite element system Solve the sparse linear system Axb, where b may be a vector or a matrix.
SOLUTION VECTORS FOR SPARSE LINEAR EQUATION SYSTEMS FULL
Iterative Solvers 1 - Krylov subspaces, Arnoldi Iteration and the Full Orthogonalisation Method The need for sparse linear algebra - A PDE exampleĪn introduction to sparse linear system solvers GPU accelerated evaluation of particle sums Welcome to Techniques of High-Performance Computing


 0 kommentar(er)
0 kommentar(er)
